
With and, we now have a system of two equations in the variables ?b? and ?c?.Įliminate the parentheses, and combine like terms.Īctually, it isn’t impossible, but if something like that happens, it means that the original system of three equations has no solution. Now we’ll subtract equation from equation. This time we need to multiply equation by ?4?, so we can subtract it from equation and eliminate the variable ?a?. We need to get another equation in only the variables ?b? and ?c?. Now let’s subtract equation from equation, which will give us an equation in only the variables ?b? and ?c?.Įliminate the parentheses, and then combine like terms. Let’s multiply equation by ?3?, so we can eliminate the variable ?a? by subtracting the resulting equation from equation. So we’ll need to multiply one of the equations by some number such that by combining the resulting equation with one of the other two equations, we’ll be able to eliminate a variable. None of the terms with the same variable have the same coefficient (or coefficients that are equal in absolute value but opposite in sign). Use any method to solve the system of equations. If you’re familiar with matrices, Gaussian Elimination is a wonderful way to solve three-variable systems of equations as well as systems with more variables and more. Now choose one of the three original equations, and plug in ?-1? for ?x? and ?-4? for ?z?, and then solve for ?y?. If we add these two equations, we can eliminate the variable ?z?, and then solve for ?x?.Ĭhoose one of the new equations, and plug in ?-1? for ?x?, and then solve for ?z?. The coefficients of ?z? in our two new equations are ?-2? and ?2?, respectively. You might have also noticed that the coefficients of ?y? in equations and are ?-5? and ?5?, respectively, so we can add these two equations to get another equation in only the variables ?x? and ?z?. Remove parentheses and combine like terms. If we add these two equations, the ?y? terms will cancel (we’ll eliminate the variable ?y?) and we’ll get an equation in only the variables ?x? and ?z?. In going from (1) to (2) we multiplied by the expressions x + y and x -3.Notice that the coefficients of ?y? in equations and are ?-5? and ?5?, respectively.
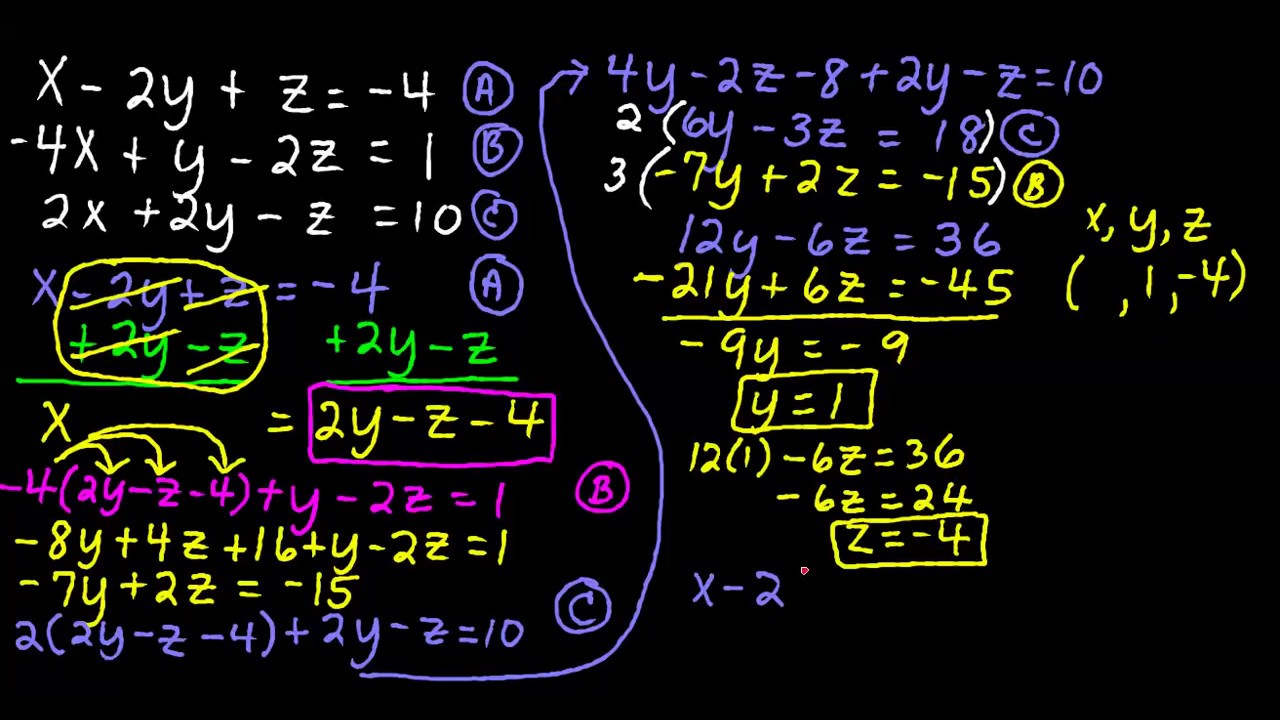
Step 2: Then substitute the expression for that.
#SYSTEM OF EQUATIONS SOLVER 3 HOW TO#
Here is the detailed strategy for how to solve systems of equations with three variables. Substituting, we obtain (5/3, -1/3) as the solution of (2). System of linear equations with three equations in three unknowns can be solved by making two substitutions. Multiply the first equation by -1 and add. We conclude this section with two examples of systems that lead to systems of linear equations. Since the second equation is satisfied for all (x, y), the solution set of system is the same as the solution set of the first equation, namely, Multiply the first equation by 1/2 and add it to the second equation to obtain the system This is the three dimensional analogue of Section 14.3.3 in Differential Equations with MATLAB.Think of as the coordinates of a vector x. Since the second equation obviously has no solution, this system, and hence the original system, is inconsistent. I need to use ode45 so I have to specify an initial value.

Thus the solution set of the original system isĪdd -2 times the first equation to the second equation to obtain the system The method of solution by elimination depends on the elementary operations E1, E2, and E3 below, which change a given system into an equivalent system.Į.1 Interchange any two equations of the system.Į.2 Multiply any equation by a nonzero number.Į.3 Replace any equation of the system by the sum of that equation and a multiple of another equation of the system.Īpplying E.3 we multiply the first equation by -2 and add it to the second equation obtaining the systemĪpply E.2 to the second equation by multiplying by -1/5. Click on "Solve Similar" button to see more examples. Let’s see how our math solver solves this and similar problems. The original system is therefore inconsistent. We write A, the solution set of the system is If A and Bare sets, then we say that A is a subset of B if each element of A is also an element of B.
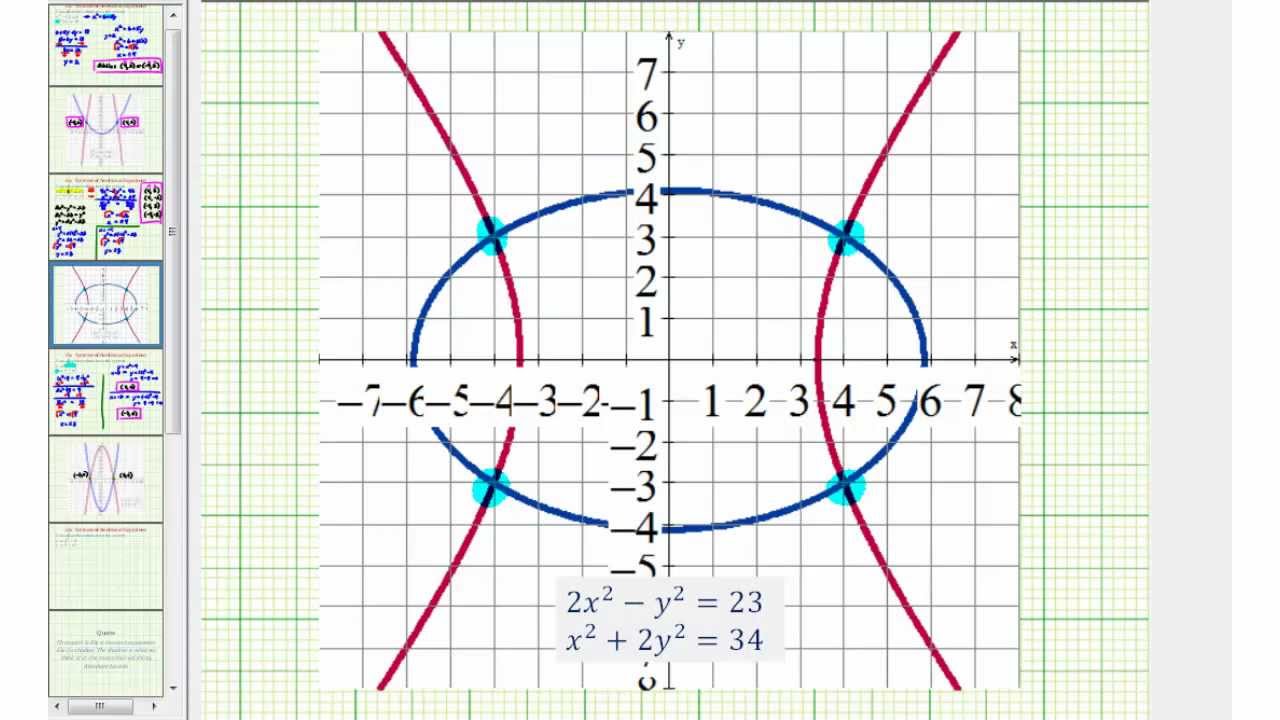
In order to better understand the concept of solving a system of equations, we will need to become familiar with some facts on sets.


 0 kommentar(er)
0 kommentar(er)
